中级工商管理辅导:企业经营决策的方法
企业经营决策的科学性必须以科学的经营决策方法作为保证。科学的企业经营决策方法是人们对决策规律的理解和把握,是具体解决决策问题的手段或工具。科学经营决策方法一般分为定性决策方法和定量决策方法。
(一)定性决策方法
定性决策方法,也称主观决策法。这种方法是直接利用人们的知识、智慧和经验,根据已掌握的有关资料对决策的内容进行分析和研究,对决策的方案进行评价和选优。定性决策方法主要有下述几种:
1.头脑风暴法
头脑风暴法又称思维共振法,即通过有关专家之间的信息交流,引起思维共振,产生组合效应,从而形成创造性思维。在典型的头脑风暴法会议中,决策者以一种明确的方式向所有参与者阐明问题,使参与者在完全不受约束的条件下,敞开思路,畅所欲言。在一定的时间内“自由”提出尽可能多的方案,不允许任何批评,并且所有方案都当场记录下来,留待稍后再讨论和分析。
头脑风暴法的目的在于创造一种畅所欲言、自由思考的氛围,诱发创造性思维的共振和连锁反应,产生更多的创造性思维。头脑风暴法对预测有很高的价值,但这种方法本身仍有缺点和弊端,即受心理因素影响较大,易屈服于权威或大多数人的意见,而忽视少数派的意见。
2.德尔菲法
德尔菲法是由美国著名的兰德公司首创并用于预测和决策的方法。该法以匿名方式通过几轮函询征求专家的意见,预测组织小组对每一轮的意见进行汇总整理后作为参考再发给各专家,供他们分析判断,以提出新的论证。几轮反复后,专家意见渐趋一致,最后供决策者进行决策。
运用德尔菲法的关键在于:第一,选择好专家,这主要取决于决策所涉及的问题或机会的性质;第二,决定适当的专家人数,一般10~50人较好;第三,拟订好意见征询表,因为它的质量直接关系到决策的有效性。现在这种方法普遍运用于政府机构、企业及各类组织中。
3.名义小组技术
名义小组技术是指以一个小组的名义来进行集体决策,而并不是实质意义上的小组讨论,要求每个与会者把自己的观点贡献出来,其特点是背靠背,独立思考。决策者首先召集具备一定知识和经验的与会者,把要解决的问题的关键内容告诉他们,要求每个人独立地将自己的想法罗列出来。而后再按次序让与会者一个接一个地陈述自己的观点或方案,每次每个成员只能提出一个观点或方案,不断循环,直到把所有人的观点都涵盖完。与会者绝对不允许对他人的观点加以反驳,只能尽可能多地罗列观点。除非是请求解释观点,否则,与会者不可以和其他人交谈,交流观点。在此基础上,由小组成员对提出的全部观点或方案进行投票,根据投票的结果,确定最终的决策方案。尽管如此,企业决策者最后仍有权决定是否接受这一方案。
(二)定量决策方法
定量决策方法是利用数学模型进行优选决策方案的决策方法。根据数学模型涉及的决策问题的性质,或者说根据所选方案结果的可靠性的不同,定量决策方法一般分为确定型决策方法、风险型决策方法和不确定:型决策方法三类。
1.确定型决策方法
确定型决策方法是指在稳定可控条件下进行决策,只要满足数学模型的前提条件,模型就能给出特定的结果。属于确定型决策方法的模型很多,这里主要介绍线性规划法和盈亏平衡点法。
(1)线性规划法。企业在进行经营决策时将面临其所能利用的资源具有稀缺性,因此必须考虑如何将有限的资源合理地投入和运用,为企业取得最好的经济效益。当资源限制或约束条件表现为线性等式或不等式,目标函数表示为线性函数时,可运用线性规划法进行决策。
线性规划法是在线性等式或不等式的约束条件下,求解线性目标函数的最大值或最小值的方法。运用线性规划法建立数学模型的步骤是:首先,确定影响目标的变量;其次,列出目标函数方程;再次,找出实现目标的约束条件;最后,找出使目标函数达到最优的可行解,即为该线性规划的最优解。
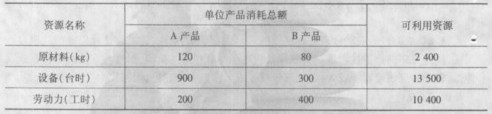
【例1】某企业生产两种产品,A产品每台利润100元,B产品每台利润180元,有关生产资料如表1—2所示,试求企业利润最大时两种产品的产量。
表1—2 A、B产品生产用料
具体计算方法如下:
设X1为A产品的生产数量,X2为B产品的生产数量。
P(Xi)为企业利润函数,i=l,2
使企业利润最大时的目标函数为:
max P(Xi)=100X1 180X2
约束条件为:
120X1 80X2≤2 400
900X1 300X2≤13 500
200X1 400X2≤10 400
X1 ≥0,X2≥0
用图解法求解,如图l—7所示。分别以X1、X2为横纵坐标,将约束方程绘制于图中,目标函数的最大值一定在由约束方程构成的可行解区域的凸点上。
通过计算四个凸点A、B、C、D所对应的目标函数值,则满足使目标函数最大值的点为B点。即当生产A产品4台、B产品24台时企业获得的利润最大,为4 720元。
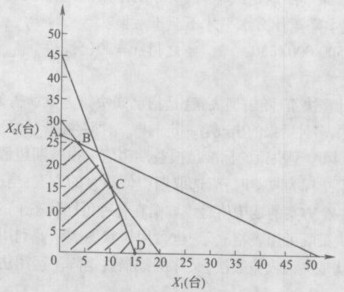
图1—7线性规划图