问:哪种方案最好?
绘制该问题的决策树,如图1一9所示。
方案l(结点①)的期望收益为:[0.7×100 0.3×(一20)]×10—300=340(万元)
方案2(结点②)的期望收益为:(0.7×40 0.3×30)×10一140=230(万元)
至于方案3,由于结点④的期望收益465(=95×7—200)万元大于结点⑤的期望收益280(=40×7)万元,所以销路好时,扩建比不扩建好。方案3(结点③)的期望收益为:(0.7×40×3 0.7×465 0.3×30×10)一140=359.5(万元)
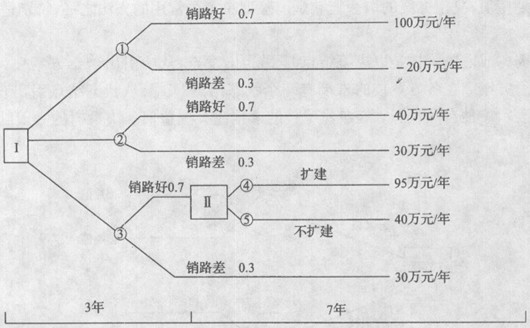
图1—9 决策树
计算结果表明,在三种方案中,方案3最好。
需要说明的是,在上面的计算过程中,我们没有考虑货币的时间价值,这是为了使问题简化。但在实际中,多阶段决策通常要考虑货币的时间价值。
3.不确定型决策方法 。
不确定型决策是指在决策所面临的自然状态难以确定而且各种自然状态发生的概率也无法预测的条件下所做出的决策。由于自然状态下决策结果的不可知,因此具有极大的风险性和主观随意性。不确定型决策常遵循以下几种思考原则。
(1)乐观原则。乐观原则是指愿承担风险的决策者在方案取舍时以各方案在各种状态下的最大损益值为标准(即假定各方案最有利的状态发生),在各方案的最大损益值中取最大者对应的方案。
【例6】 某企业拟开发新产品,有三种设计方案可供选择。因不同的设计方案的制造成本、产品性能各不相同,在不同的市场状态下的损益值也各异。有关资料如表l—4所示:
表1—4 数据表
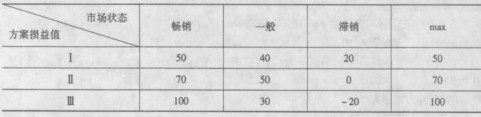
在不知道各种状态的概率时,用乐观原则选择方案的过程如下:
①在各方案的损益中找出最大者;
②在所有方案的最大损益值中找最大者,即max{50,70,100}=100,它所对应的方案Ⅲ就
是用该原则选出的方案。
(2)悲观原则。悲观原则是指决策者在进行方案取舍时以每个方案在各种状态下的最小值为标准(即假定每个方案最不利的状态发生),再从各方案的最小值中取最大者对应的方案。
仍以上表资料为例,用悲观原则决策时先找出各方案在各种状态下的最小值,即{20,0,-20},然后再从中选取最大值:max{20,0,-20}=20,对应的方案I即为用悲观原则选取的决策方案。该方案能保证在最坏情况下获得不低于20单位的收益,而其他方案则无此保证。
(3)折中原则。悲观原则和乐观原则都是以各方案不同状态下的最大或最小极端值为标准的。但多数情况下决策者既非完全的保守者,亦非极端冒险者,而是在介于两个极端的某一位置寻找决策方案,即折中原则。折中原则的决策步骤如下: