①找出各方案在所有状态下的最小值和最大值;
②决策者根据自己的风险偏好程度给定最大值系数α(0<α<1),最小值的系数随之被确定为1一α,α也叫乐观系数,是决策者乐观程度的度量;
③用给定的乐观系数仅和对应的各方案最大最小损益值计算各方案的加权平均值;
④取加权平均最大的损益值对应的方案为所选方案。
仍以以上所给数据资料为例,计算各方案的最小值和最大值,如表1—5所示:
设决策者给定最大值系数α=0.75,最小值系数即为0.25,各方案加权平均值如下:
Ⅰ:20×0.25 50 ×0.75=42.5
Ⅱ:0×0.25 70 ×0.75=52.5
Ⅲ:(-20)x0.25 100×0.75=70
表1—5 收益值比较表

取加权平均值最大者:max{42.5,52.5,70}=70,对应的方案llI即为最大值系数α=0.75 时的折衷原则方案。
用折中原则选择方案的结果,取决于反映决策者风险偏好程度的乐观系数的确定。上例中,如α取0.2,1-0.2=0.8,方案的选择结果是I而非Ⅲ。当α=0时,结果与悲观原则相同;当α=1时,结果与乐观原则相同。这样,悲观原则与乐观原则便成为折中原则的两个特例。
(4)后悔值原则。后悔值原则是用后悔值标准选择方案。后悔值是指在某种状态下因选择某方案而未选取该状态下的最佳方案而少得的收益。用后悔值法进行方案选择的步骤如下:
①计算损益值的后悔值矩阵,方法是用各状态下的最大损益值分别减去该状态下所有方案的损益值,从而得到对应的后悔值;
②从各方案中选取最大后悔值;
③在已选出的最大后悔值中选取最小值,对应的方案即为用最小后悔值法选取的方案。
仍以上例资料为例,计算出的后悔值矩阵如表l—6所示。
表l一6 最大后悔值比较表
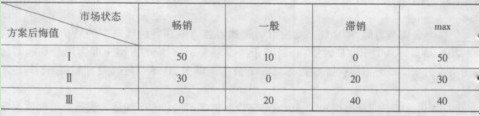
各方案的最大后悔值为{50,30,40},取其最小值rain{50,30,40}=30,对应的方案Ⅱ即为用最小后悔值原则选取的方案。
(5)等概率原则。等概率原则是指当无法确定某种自然状态发生的可能性大小及其顺序时,可以假定每一自然状态具有相等的概率,并以此计算各方案的损益值,进行方案选择。假设各种方案产生的概率相同,通过比较每个方案的损益值的平均值来进行方案的选择。在利润最大化的目标下,将选择平均利润最大的方案;而在成本最小化的目标下,将选择平均成本最小的方案。
仍以上例资料为例,各方案有三种状态,每种状态的概率为1/3,各方案的平均值为:
I:50×l/3 40×1/3 20 x 1/3=l 10/3
Ⅱ:70×l/3 50×l/3 0×l/3=40
Ⅲ:100×1/3 30×1/3 (一20)‘×l/3=l 10/3
max{110/3,40,110/3}=40
所以,应选方案Ⅱ。
按照等概率原则进行决策,在于将结果建立在平均分配的基础上,必然与实际情况产生偏差,往往会给组织活动带来不利影响。
