相对数或平均数时间序列序时平均数的计算
相对数或平均数时间序列是派生数列,相对数或平均数通常是由两个绝对数对比形成的。
计算思路:分别求出分子指标和分母指标时间序列的序时平均数,然后再进行对比,用公式表示如下:
![]()
增长量:报告期发展水平与基期发展水平之差,反映报告期比基期增加(减少)的绝对数量。
用公式表示为:增长量=报告期水平-基期水平
(1)逐期增长量-----报告期水平与前一期水平之差
(2)累计增长量-----报告期水平与某一固定时期(通常是时间序列最初水平)水平之差。
注意:同一时间序列中,累计增长量等于相应时期逐期增长量之和。
平均增长量
平均增长量是时间序列中逐期增长量的序时平均数,它表明现象在一定时段内平均每期增加(减少)的数量。其计算公式为:
平均增长量=![]()
发展速度
1、发展速度:是以相对数形式表示的两个不同时期发展水平的比值,表明报告期水平已发展到基期水平的几分之几或若干倍。
发展速度= ![]()
由于基期选择的不同,发展速度有定基与环比之分。

(3)定基发展速度与环比发展速度之间的关系
第一,定基发展速度等于相应时期内各环比发展速度的连乘积:
推导:定基发展速度![]() =各环比发展速度的连乘积
=各环比发展速度的连乘积
第二,两个相邻时期定基发展速度的比率等于相应时期的环比发展速度
推导:
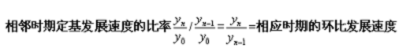

平均发展速度:反映现象在一定时期内逐期发展变化的一般程度。
平均发展速度是一定时期内各期环比发展速度的序时平均数。
目前计算平均发展速度通常采用几何平均法。
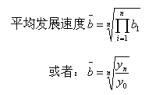
n表示环比发展速度的时期数。
2、平均增长速度:反映现象在一定时期内逐期增长(降低)变化的一般程度。
3、平均发展速度与平均增长速度的关系:
平均增长速度=平均发展速度-1
增长1%的绝对值”是进行这一分析的指标。它反映同样的增长速度,在不同时间条件下所包含的绝对水平。
