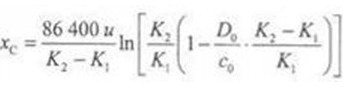2.河流的一维稳态水质模式。对于溶解态污染物,当污染物在河流横向方向上达到完全混合后,描述污染物的输移、转化的微分方程为:
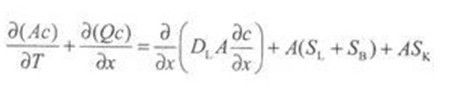
式中:A—河流横断面面积:Q—河流流量;c—水质组分浓度;DL—综合的纵向离散系数;SL—直接的点源或非点源强度:SB—上游区域进入的源强; SK—动力学转化率,正为源,负为汇。
设定条件:稳态(∂/∂t=0),忽略纵向离散作用,上述微分方程的解:c=c0exp[-Kx/(86400u)] (6-7)
式中:c0—初始浓度,按点源河流完全混合模式求得,mg/L;u—河流流速,m/s;x—从计算初始点到下游计算断面的距离,m;c—计算断面的污染物浓度,mg/L.
3.Streeter-Phelps模式。是研究河流溶解氧与BOD关系的最早的、最简单的耦合模型。它的基本假设为:河流为一维恒定流,污染物在河流横断面上完全混合;氧化和复氧都是一级反应,反应速率常数是定常的,氧亏的净变化仅是水中有机物耗氧和通过液-气界面的大气复氧的函数。Streeter-Phelps模式:
c=c0exp[-K1x/(86400u)]
D=[K1c0/(K2-K1)]{exp[-K1x/(86400u)]-exp[-K2x/(86400u)]} D0exp[-K2x/(86400u)] (6-8)
其中,c0= (cpQp chQh)/(Qp Qh) (6-9) D0= (DpQp DhQh)/(Qp Qh) (6-10)
式中:Qp—废水排放量,m3/s;Qh—河流流量,m3/s;D—亏氧量即DOf-DO,mg/L;D0—计算初始断面亏氧量,mg/L;Dp、Dh—污水、上游来水中溶解氧亏值,mg/L;u—河流断面平均流速,m/s;X—沿程距离,m;c—沿程浓度,mg/L.DO、DO
f—溶解氧、饱和溶解氧浓度,mg/L;K1、K2—耗氧、复氧系数,1/d. 临界氧亏点xC的位置为: